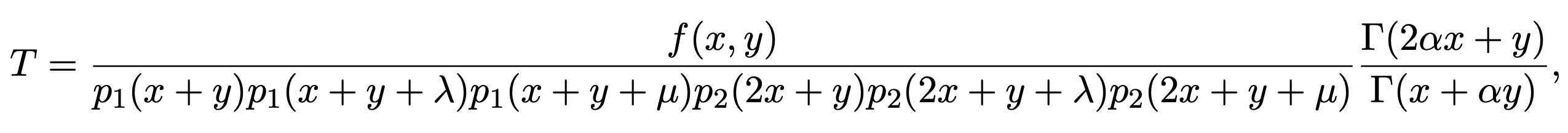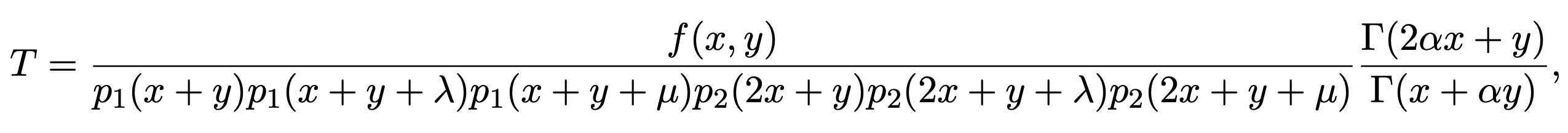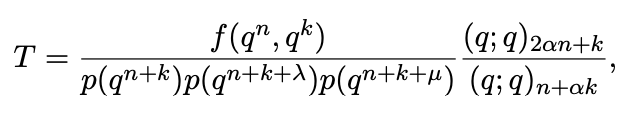A Unified Reduction for Hypergeometric and q-Hypergeometirc Creative Telescoping
Supplementary material to the paper
A Unified Reduction for Hypergeometric and q-Hypergeometirc Creative Telescoping
by Shaoshi Chen, Hao Du, Yiman Gao, Hui Huang, and Ziming Li.
Software
We provide prototype Maple implementations and the corresponding Maple notebooks
for both the usual shift and the q-shift cases:
Timings
We have compared the algorithms from our paper with Zeilberger's algorithm and its q-analogue, respectively.
All timings were measured in seconds on a macOS computer with 32GB RAM and 2.3GHz Quad-Core Intel Core i7 processors.
The computations for the experiments did not use any parallelism.
The usual shift case
We considerd bivariate hypergeometric terms of the form
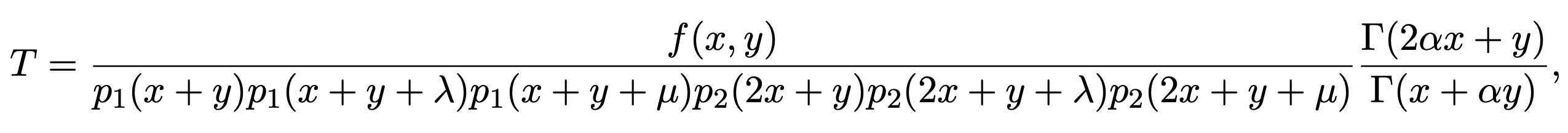
where f is a bivariate polynomial in x and y over integers of total degree n,
p1, p2 are both univariate polynomials over integers of degree m,
and α, λ, μ are all nonnegative integers.
For a selection of random terms of this type for different choices of m, n, α, λ, μ,
the table below collects the timings of the related algorithms applied to the given hypergeometric term,
in which
-
Z: the command Zeilberger in the Maple built-in package SumTools[Hypergeometric],
yielding a minimal telescoper and a corresponding certificate.
-
HTC: the command HypergeomTelescoping in the Maple package HypergeometricCT,
yielding a minimal telescoper and a corresponding certificate.
-
HT: the command HypergeomTelescoping in the Maple package HypergeometricCT,
yielding a minimal telescoper without computing a certificate.
-
order: the order of the resulting minimal telescoper.
-
Telescoper: the computed minimal telescoper.
| Example |
(m, n, α, λ, μ) |
Z |
HTC |
HT |
order |
Telescoper |
|
example1
|
(1, 0, 1, 5, 5) |
9.66 |
1.22 |
0.38 |
4 |
tele1
|
|
example2
|
(1, 0, 2, 5, 5) |
34.10 |
4.72 |
1.33 |
6 |
tele2
|
|
example3
|
(1, 0, 3, 5, 5) |
151.94 |
15.32 |
3.97 |
7 |
tele3
|
|
example4
|
(1, 8, 3, 5, 5) |
346.26 |
27.98 |
7.77 |
7 |
tele4
|
|
example5
|
(2, 0, 1, 5, 10) |
104.86 |
7.18 |
1.63 |
4 |
tele5
|
|
example6
|
(2, 0, 2, 5, 10) |
338.58 |
24.80 |
6.94 |
6 |
tele6
|
|
example7
|
(2, 0, 3, 5, 10) |
1094.61 |
57.67 |
13.80 |
7 |
tele7
|
|
example8
|
(2, 3, 3, 5, 10) |
1417.06 |
65.51 |
18.42 |
7 |
tele8
|
|
example9
|
(2, 0, 1, 10, 15) |
1056.24 |
15.80 |
2.90 |
4 |
tele9
|
|
example10
|
(2, 0, 2, 10, 15) |
1221.96 |
73.73 |
15.98 |
6 |
tele10
|
|
example11
|
(2, 0, 3, 10, 15) |
4324.55 |
178.24 |
50.72 |
7 |
tele11
|
|
example12
|
(2, 5, 3, 10, 15) |
4057.58 |
179.14 |
42.46 |
7 |
tele12
|
|
example13
|
(3, 0, 1, 5, 10) |
6590.60 |
32.06 |
8.34 |
6 |
tele13
|
|
example14
|
(3, 0, 2, 5, 10) |
12876.37 |
145.67 |
46.26 |
8 |
tele14
|
|
example15
|
(3, 0, 3, 5, 10) |
53350.14 |
458.99 |
132.26 |
9 |
tele15
|
The q-shift case
We considerd bivariate q-hypergeometric terms of the form
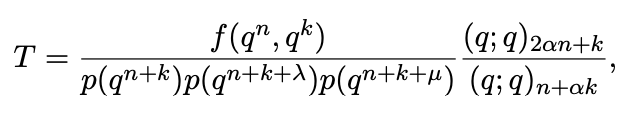
where f is a bivariate polynomial in qn and qk over rational functions in q
of total degree 1, p is a univariate polynomial over rational numbers of degree d,
and α, λ, μ are all nonnegative integers.
For a selection of random terms of this type for different choices of d, α, λ, μ,
the table below collects the timings of the related algorithms applied to the given q-hypergeometric term,
in which
-
qZ: the command Zeilberger in the Maple built-in package QDifferenceEquations,
yielding a minimal telescoper and a corresponding certificate.
-
qHTC: the command QHypergeomTelescoping in the Maple package QHypergeometricCT,
yielding a minimal telescoper and a corresponding certificate.
-
qHT: the command QHypergeomTelescoping in the Maple package QHypergeometricCT,
yielding a minimal telescoper without computing a certificate.
-
order: the order of the resulting minimal telescoper.
| Example |
(d, α, λ, μ) |
qZ |
qHTC |
qHT |
order |
Telescoper |
|
qexample1
|
(1, 1, 1, 5) |
0.72 |
0.60 |
0.35 |
2 |
qtele1
|
|
qexample2
|
(1, 2, 1, 5) |
4231.61 |
1361.15 |
687.13 |
5 |
qtele2
|
|
qexample3
|
(2, 1, 1, 5) |
12.54 |
6.17 |
2.54 |
3 |
qtele3
|
|
qexample4
|
(2, 2, 1, 5) |
152422.70 |
15205.41 |
8035.85 |
6 |
qtele4
|
|
qexample5
|
(3, 1, 1, 5) |
564.80 |
53.45 |
15.69 |
4 |
qtele5
|
|
qexample6
|
(1, 1, 5, 10) |
9.99 |
5.29 |
1.58 |
2 |
qtele6
|
|
qexample7
|
(1, 2, 5, 10) |
31415.79 |
15629.64 |
6776.37 |
5 |
qtele7
|
|
qexample8
|
(1, 1, 10, 15) |
42.40 |
35.55 |
5.78 |
2 |
qtele8
|
Last modified: May 2024.